Great Circles, Black Holes, and Community Events Part 3 of 3

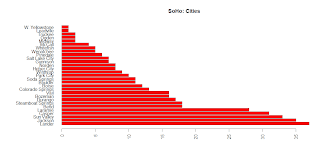
The second community event is the Soldier Hollow Junior Olympics (SoHo), again found in the Heber Valley area. Building upon the previous posts (part 1 and part 2) this one will show an event that has more people coming from greater distance. Take the bar charts for the number of participants and the cities they are from. Instead of 2 major cities (Heber Valley Railroad), SoHo has several cities and states with many participants for each.

The histogram for distance shows a similar pattern, where with the railroad it was a nice log looking distribution, this is a little more even. The second histogram is a zoomed in and the bins expanded for greater detail.

While the map is not as great as the railroad, which is why the distance histogram is so important, it does show a good representation of the northwestern states. Unlike the railroad map, each line does represent more participants than 3.

What makes this tool so great is the ability to visually show the interaction between distance, number of participants, and the draw of an event. The numbers are nothing really new, but the charts are what make this analysis shine. When talking to community representatives whose education range from high school graduate to PhD, pictures are critical.

#Soldier Hallow Analysis

soho<-read.csv(file.choose(), header=TRUE)
summary(soho)
table.city<-sort(table(soho$city), decreasing=TRUE)
table.st<-sort(table(soho$state), decreasing=TRUE)

par(mar=c(5, 11, 4, 2), las=2)
barplot(table.city, main=‘SoHo: Cities’, horiz=TRUE, col=‘red’)

par(mar=c(5, 4, 4, 2), las=2)
barplot(table.st, main=‘SoHo: States’, horiz=TRUE, col=‘red’)

heber<-c(-111.33259, 40.511413)
soho.data<-matrix(data=c(soho$long, soho$lat), nrow=373, ncol=2)
soho.ut<-subset(soho, subset=(state==‘UT’))
soho.data.ut<-matrix(data=c(soho.ut$long, soho.ut$lat), nrow=29, ncol=2)
soho.dist<-(distm(heber, soho.data, fun=distVincentyEllipsoid)*0.000621371192)
soho.dist.ut<-(distm(heber, soho.data.ut, fun=distVincentyEllipsoid)*0.000621371192)
dist.soho<-matrix(soho.dist, nrow=373, ncol=1)
dist.soho.ut<-matrix(soho.dist.ut, nrow=29, ncol=1)
summary(dist.soho)
sd(dist.soho)
p.skew.soho<-(3*(mean(dist.soho)-median(dist.soho)))/sd(dist.soho)
hist(dist.soho, main=‘SoHo: Distance Histogram’, col=‘red’)
hist(dist.soho.ut, main=‘SoHo: Distance Histogram Utah’, breaks=20, col=‘red’)

#mapping it out
#US
map("state", col="#f2f2f2", fill=TRUE, bg="white", lwd=0.25)
title(main=‘SoHo: US Map’)
for(i in 1:dim(soho.data)[1]){
 inter <- gcIntermediate(heber, soho.data[i, 1:2], n=373, addStartEnd=TRUE)
 lines(inter, col="red")
}
 
#Zoomed into West
par(mfrow=c(1,2), mar=c(5,4,4,2))
map("state", col="#f2f2f2", fill=TRUE, bg="white", lwd=0.25, xlim=c(-125, -103), ylim=c(30, 50))
title(main=‘SoHo: Western Region’)
 
for(i in 1:dim(soho.data)[1]){
 inter <- gcIntermediate(heber, soho.data[i, 1:2], n=373, addStartEnd=TRUE)
 lines(inter, col="red")
}

#Utah
map("state", col="#f2f2f2", fill=TRUE, bg="white", lwd=0.25, xlim=c(-112.1, -111), ylim=c(40, 42))
title(main=‘SoHo: Utah’)
for(i in 1:dim(soho.data.ut)[1]){
 inter <- gcIntermediate(heber, soho.data.ut[i, 1:2], n=29, addStartEnd=TRUE)
 lines(inter, col="red")
}
par(mfrow=c(1,1))

Created by Pretty R at inside-R.org

Great Circles, Black Holes, and Community Events Part 2 of 3

This post will examine the Heber Valley Railroad, a small town tourist attraction using event gravitational pull. Using the information from part 1 the two factors associated with the events gravity, the number of participants, and the distance they traveled. The number of participants can be shown using bar charts, histograms, and summary tables. The distance traveled can be displayed using bar charts, histograms, summary charts, and most important great circle maps. Below are some of the charts I created when doing the analysis.

The first two are bar charts show where the majority of train riders are coming from. From the graphs Salt Lake City Utah is number one, followed by Ogden, then it goes down hill from there very quickly. The purpose of these first graphs is to show how many people are coming to the event and where.

Where the first set of graphs show the cities, the histograms show where people are coming from in terms of distance. The first histogram shows all the data, the next two are zoomed in to show the majority of people travel less than 100 miles (as the crow flies) to get to the train. While the majority of people who ride the train do so within 100 miles, there are many who travel many miles. But it should be noted, there are only 1-3 customers per line. The map looks really good, but the majority of those traveling long distances, are much fewer.

While the map shows a number of people coming from various locations, there are only 1-3 people per line, nothing to really spend any marketing funds to. The map does show how far people do come.

The next two maps show that within Utah the majority of people riding the train come from Salt Lake, Ogden, and the Wasatch Front area.

require(geosphere)
require(maps) 
 
#HVRR Analysis
#Step 1: basic Stats. Summaries, Histograms, bar charts
#reading the file in
 
hvrr<-read.table(file.choose(), header=TRUE)
 
#summary stats
summary(hvrr)
 
#histograms
par(mfrow=c(1,2))
label.1<-c(‘Utah (424 88%)’, ‘Other(58 12%)’)
state<-c(424, 58)
barplot(state, names.arg=label.1, main=‘HVRR: States’, col=‘blue’)
label.2<-c(‘Salt Lake’, ‘Ogden’, ‘Other’)
cities<-c(173, 102, 149)
barplot(cities, names.arg=label.2, main=‘HVRR: Cities Within Utah’, col=‘blue’)
par(las=2, mar=c(5,12,4,2), mfrow=c(1,1))
city.1<-sort(table(hvrr$city))
city.1<-tail(city.1, n=20)
barplot(city.1, col=‘blue’, hor=TRUE, main=‘HVRR: Utah Cities Top 20’)
par(las=0, mar=c(5,4,4,2))
 
#distance analysis
heber<-c(-111.33259, 40.511413)
data<-matrix(data=c(hvrr$long, hvrr$lat), nrow=482, ncol=2)
ut<-subset(hvrr, subset=(st==‘UT’))
data.ut<-matrix(data=c(ut$long, ut$lat), nrow=424, ncol=2)
dist<-(distm(heber, data, fun=distVincentyEllipsoid)*0.000621371192)
dist.rr<-matrix(dist, nrow=482, ncol=1)
hvrr<-cbind(hvrr, dist.rr)
 
#histograms of various shapes and zooms
summary(dist.rr)
par(mfrow=c(1, 3))
hist(dist.rr, breaks=12, main=‘HVRR Distances: 0-3,000 miles’, xlab=‘Distance in Miles’, col=‘blue’)
hist(dist.rr, breaks=24, main=‘HVRR Distances: 0-500 miles’, xlab=‘Distance in Miles’, xlim=c(0, 500), col=‘blue’)
hist(dist.rr, breaks=50, main=‘HVRR Distances: 0-200 miles’, xlab=‘Distance in Miles’, xlim=c(0, 200), col=‘blue’)
par(mfrow=c(1,1))
 
#mapping it out
 
#US
map("world", col="#f2f2f2", fill=TRUE, bg="white", lwd=0.25, xlim=c(-158, -65), ylim=c(15, 50))
title(main=‘HVRR: US Map’)
for(i in 1:dim(data)[1]){
 inter <- gcIntermediate(heber, data[i, 1:2], n=482, addStartEnd=TRUE)
 lines(inter, col="blue")
}
 
#Zoomed into Utah
par(mfrow=c(1,1), mar=c(5,4,4,2))
map("state", col="#f2f2f2", fill=TRUE, bg="white", lwd=0.25, xlim=c(-115, -108), ylim=c(37, 42))
title(main=‘HVRR: Utah’)
for(i in 1:dim(data.ut)[1]){
 inter <- gcIntermediate(heber, data.ut[i, 1:2], n=424, addStartEnd=TRUE)
 lines(inter, col="blue")
}
 
#Wasatch Front
map("state", col="#f2f2f2", fill=TRUE, bg="white", lwd=0.25, xlim=c(-112.5, -111), ylim=c(40, 42))
title(main=‘HVRR: Utah- Wasatch Front’)
for(i in 1:dim(data.ut)[1]){
 inter <- gcIntermediate(heber, data.ut[i, 1:2], n=424, addStartEnd=TRUE)
 lines(inter, col="blue")
}
par(mfrow=c(1,1))

Created by Pretty R at inside-R.org

Great Circles, Black Holes, and Community Events Part 1 of 3

About 8 years ago, I was sitting in class listening to a guest lecturer talk about how community events can be described like celestial bodies with their own gravity, where the size and importance of the event would attract more people, from farther away. Much like a black hole, where the bigger the mass of the black hole the higher the gravity.

In physics gravity is a constant, for a community event the gravity can be determined by using the number of participants, and the distance traveled. Where the higher the number of participants and the greater the distance traveled would show an event with higher gravity. For example, a farmers market where only the locals come, versus an international conference of some kind. Assuming both events attract the same number of people, the international conference would have the higher gravity as there would be a larger distance traveled.

Of the two elements the number of participants can be easily found; either by number of seats sold, tickets, counting the number of people present, and so on. The more difficult information is to determine the distance traveled. For this two points are needed, the event (destination) and the point of origin (person's home). The most accurate method would be to get a GPS coordinate for every home, but this would be very difficult mainly because most people do not know what it is, and second they are probably not willing to divulge such information. Another alternative is to request address, again people are becoming much more savvy about personal information, as they should be, and getting a good sample might be problematic. The solution then lies with the zip code, a number with the required latitude and longitude numbers that is broad enough so people do not feel their privacy is being invaded, while still being able to determine a reasonable distance number for each participant.

Using the zip code, and the associated lat and long information the numbers can then be put into R code to draw fantastic maps using the great circle inspired by Oscar Perpiñán Lamigueiro. One question did come out of the data and that is which of the several methods to use when drawing and determining the distance?

The question arises out of the equations assumption on the shape of the earth. Using the Geosphere package there were three equations, the first two Haversine and Vincenty Sphere both assume the earth is round. Which as it turns out it is more elliptical, so there is the Vincenty Ellipsoid. What I wanted to know was is there a big difference between the different formulas? And if so, how big?

require(geosphere)
require(maps)
data(us.cities)
 
#Setting up the data, ‘ny’ is the long. and lat. for New York City, ‘all’ is a matrix of all the 
# cities available in the geosphere package (1005), with the long. and lat. data.
 
ny<-c(-118.41, 34.11)
all<-matrix(data=c(us.cities$long, us.cities$lat), ncol=2)
 
#Summing the distance between NY and all the other cities in the US (1005 of them)
#by so doing the error is compounded with each additional city
 
hav<-sum(distm(ny, all, fun=distHaversine))
hav.time<-proc.time()
v.sphere<-sum(distm(ny, all, fun=distVincentySphere))
v.sphere.time<-proc.time()
v.ellip<-sum (distm(ny, all, fun=distVincentyEllipsoid))
v.ellip.time<-proc.time()
hav.time; v.sphere.time; v.ellip.time;
proc.time<-c (1.350, 1.350, 2.510)
row.names<-c(‘Haversine’,’Vincenty.Sphere’, ‘Vincenty.Ellipsoid’)
ny.all<-rbind(hav, v.sphere, v.ellip); ny.all<-cbind(ny.all, proc.time)
rownames(ny.all)<-row.names; colnames(ny.all)<-c(‘Sum Distance’, ‘Processor Time’)
 ny.all
 
#Determining the difference between the various models available in the geosphere package
#Meters were conveted into miles, the largest difference between the models was approximately
#1090 miles, or 1.085326 miles per city of difference, this is considerable
 
hav.v.ellp<-(v.ellip-hav)*0.000621371192
hav.v.sphere<-abs(hav-v.sphere)*0.000621371192
hav.v.ellp; hav.v.sphere
diff<-rbind(hav.v.ellp, hav.v.sphere)
rownames(diff)<-c(‘Haversine-Vincenty.Ellipsoid’,’Haversine-Vincenty.Sphere’)
colnames(diff)<-’Distance (miles)’; diff
 
#what is the average error
 
hav.v.ellp/1005
 

Created by Pretty R at inside-R.org

In the end the Vincenty.Ellipsoid was used as the method for determining the distance as it was the most precise by an average margin of 1.0853 miles per city, this is a significant margin of error when many cities are being analyzed and the extra computing time is worth it.

The next post will show how the data can be used to analyze two different community events.